The meaning of “energy” in everyday use is simple. If I am tired, I have little energy to do anything. If I feel fresh and alert, I have plenty of energy.
In physics though, energy refers to something more er … , physical. Like:
- kinetic energy
- potential energy
- heat energy
- light energy
- electrical energy
- nuclear energy, etc
And the law the governs all of them is called Law of Conservation of Energy. It goes like this :
“Energy cannot be created or destroyed. It can only be converted from one form to another.”
This law governs all of the above energy except nuclear energy. More on that later.
This seems to me like a very abstract statement, unlike Newton’s first 2 laws on familiar forces and motion. His 3rd law is also a bit abstract. I shall talk about that in another article.
One reason the law looks is abstract is because we cannot see energy. For school students, another reason is the way it is defined in textbooks :
"Energy is the capacity to do work."
When I first saw this in textbook as a child, I wondered what it has got to do with anything – that is, anything in the subsequent explanations about energy in the book. After 40 years, as I write this, I still wonder.
I just checked the meaning of “capacity” on google – one of the meanings : “the amount that something can produce”
This seems relevant. If I replace the word capacity by this phrase in the energy definition is :
“Energy is the amount that something can produce to do work.”
That sounds awkward. How about this :
“Energy is the amount of work that something can do.”
That’s it ! That is exactly right. And that is also the simple meaning I have been looking for !
If only textbooks had written it that way. But ... "that something can do"? Maybe too colloquial for a serious textbook. Sigh !
I guess serious people just have to say things in abstract and complicated ways.
Anyway, for a student, the practical meaning of energy consists of knowing the following :
1. The law conservation of energy given above
2. Examples on the types of energy we know : potential / kinetic energy, heat, light, electricity, … except nuclear energy.
3. Perhaps more importantly – examples on how it can be converted from one form to another, e.g. mechanical to electrical.
And that is more or less how we really learn about energy and do exam questions on it. But now and then, the physics exam paper may pop up the question :
"What is energy?"
The official answer would be : "Energy is the capacity to do work."
But what if they then ask you what is “work”?? I shall leave that for another article on work, energy and power.
Now that we get the terms and definitions out of the way, lets look at something more practical :
- How do we check by measurement that energy is really conserved?
- What does this mean to our everyday life?
To appreciate the meaning, I like to think of energy as money. Lets say I have $10. I give you $3. I am left with $7. The total is still $10. So money is "conserved".
Actually, money is not conserved. Governments can print as much as they think they need.
That issue kind of happened to energy when the Americans (ok, maybe foreign scientists working in America) invented the atomic bomb. When detonated, the atomic bomb actually created more energy than before.
Some scientists started to realise this possibility when Einstein discovered E = mc2, which suggested that mass can be converted into energy.
And this was what happened in the atomic bomb. After detonation, the total mass of the explosion products is a bit smaller than the starting mass, by about the mass of a $5 bill if I remember correctly.
If I have to guess the currency, it is probably a United States $5 bill.

I digressed. But this also shows that even for laws of physics, there is limit to how widely we can apply them. When we talk about the law of energy conservation, we normally assume situations that do not involve nuclear reactions or explosion – that is to say, no change in total mass.
That is - unless the school chapter or question mentions nuclear reaction. Then we switch our mind to something called the law of conservation of mass-energy. I may talk about that in another article. Something to do with E = mc2.
What I want to talk about is how scientists actually check with experiments that energy is really conserved. And guess who is the earliest scientist (or at least one of the earliest) who checked this?
Galileo !
Where would we be without him? (Having fun instead of studying physics !?)
I am not sure if Galileo thought of energy the same way we learn about it in school physics today. Our understand of energy probably came about from scientists after Galileo, starting from around Newton’s time.
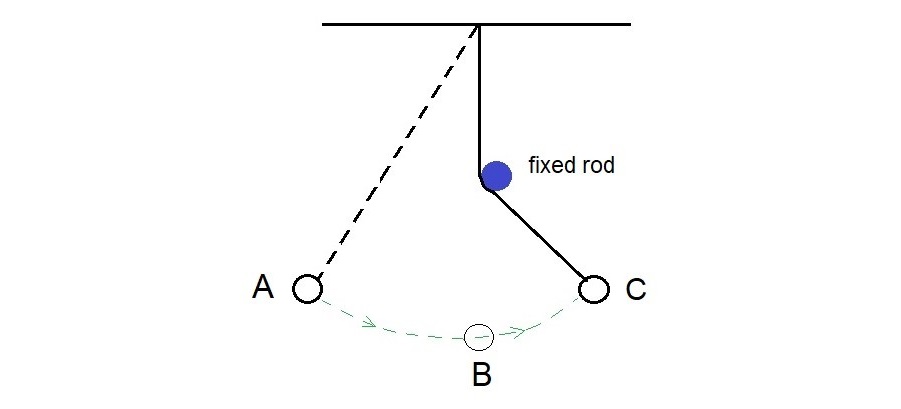
Galileo’s interrupted pendulum is a nice and simple way to demonstrate conservation of energy, though his purpose might have been just to describe how the ball moves when the thread is interrupted.
This is what the interrupted pendulum looks like.

“This is a famous experiment said to have been performed by Galileo. It was a stroke of genius. Friction made experiments with a rolling ball on a track unconvincing.”
When at rest at A, the ball has energy because of its height. The is called potential energy. You cannot see the effect of this energy. We can only tell when we let go and find that it falls.
The energy due of this movement is called kinetic energy. At the lowest point B, it moves the fastest. We find that the ball only stops when it reaches C, the same height as A.
This suggests that the potential energy due to its height at A is fully recovered at C, since potential energy depends on the vetical height.
It also suggests the kinetic energy at B, the lowest point, must have come from the potential energy at A. So maybe the drop in potential energy as the bob falls from A to B - is all converted to kinetic energy at B.
What about in between A and B? Probably some potential, some kinetic energy. And maybe if we add them, they would be same as the starting potential energy at the top at A?
I am just allowing my mind to wander – thinking what people who study physics might think about motion and energy. The above rambling may suggest that the total
stays the same as the pendulum swings between A and C – i.e. that the total energy is “conserved”.
We may also replace the pendulum string above by a perfectly smooth track the same shape as A-B-C in the figure. In this case, the same energy reasoning above may apply.
In the real world however, there would always be friction. This would slow the motion and the C may not reach the same height as A in the figure above.
The “total energy stays the same” observation above is what conservation of energy means.
The Wikipedia page on "Conservation of energy" states:
“In 1639, Galileo published his analysis of several situations—including the celebrated "interrupted pendulum"—which can be described (in modern language) as conservatively converting potential energy to kinetic energy and back again. Essentially, he pointed out that the height a moving body rises is equal to the height from which it falls, and used this observation to infer the idea of inertia. The remarkable aspect of this observation is that the height to which a moving body ascends on a frictionless surface does not depend on the shape of the surface.”
So it does not matter whether you move up on the stairs, on a string, on an inclined plane or on a curved road. Your potential energy depends only on the vertical height.
Galileo in 1639, however, did not use this to suggest the idea of energy as we know it in physics today. This was to take place among the European scientists over the next few hundred years.
Of this work, the part which I think is the most difficult and also the most clever – is the linking of mechanical energy and heat energy.
“Energy cannot be created or destroyed. It can only be converted from one form to another.”
Today, this is easier to understand. We learn in school physics that when an object is hot, the atoms and electrons in the object vibrate more. This is what makes it feel hot when we touch it. And this is what heat is about.
But how did scientists know this? Even today when we can take “photos” of atoms using something called a scanning tunneling microscope, it is not quick and simple method.
Between Galileo’s time and today, there were a number of very clever scientists (like Newton) who were interested in this “energy” idea.
“In 1639, Galileo published his analysis of several situations—including the celebrated "interrupted pendulum"—which can be described (in modern language) as conservatively converting potential energy to kinetic energy and back again. Essentially, he pointed out that the height a moving body rises is equal to the height from which it falls, and used this observation to infer the idea of inertia. The remarkable aspect of this observation is that the height to which a moving body ascends on a frictionless surface does not depend on the shape of the surface.” (Wikipedia - Conservation of energy)
This means that we can imagine replacing the string of the pendulum by a curved surface like this. The ball will roll up to the same height – as long as the surface is perfectly smooth, so that no energy is lost to friction.
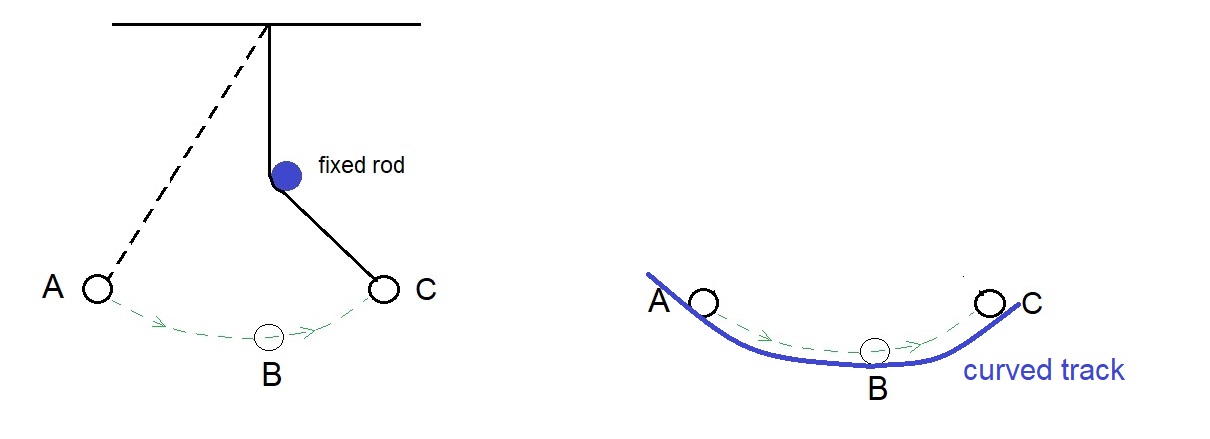
But this friction thing is troublesome. It keeps taking the kinetic energy away. We all know about friction. It is everywhere. Without friction, like on an oily ground, we cannot even walk. We would just slip and fall !
So what happens to this kinetic energy when there is friction? Is it just gone, erased, vanished, disappeared?
If you have been in a cold country, or a very cold air-con room, you or others may be seen rubbing their hands trying to keep warm. Warmth … Heat !
Somehow, this did not seem obvious to people until Count Rumford demonstrated this by drilling a canon and using the heat generated to boil water, around 1798.
Around 1840, James Joule in England used the force from a falling weight to stir water. He measured the water temperature and showed that it went up.
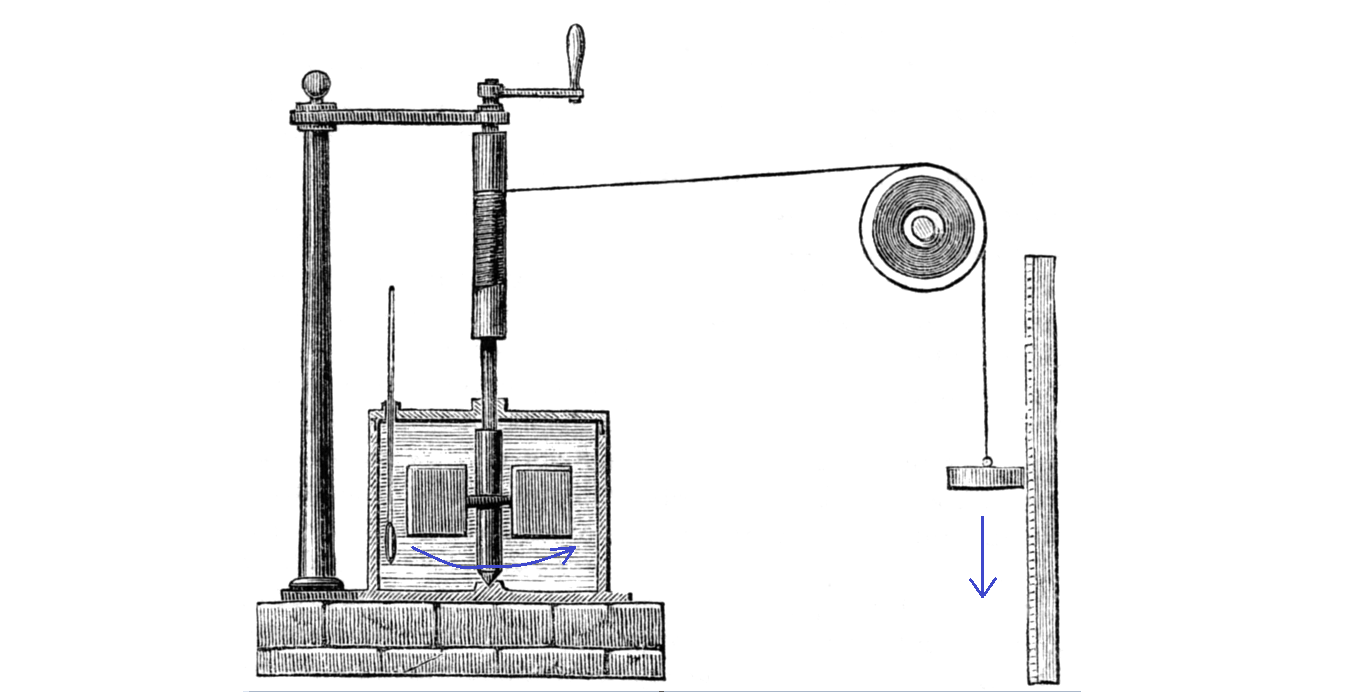
The careful measurement probably convinced people that the potential energy of the falling weight is really converted to heat energy in the water.
Now you know why the unot of energy is "joule".
But I cannot find any mention on google of an experiment to show that the heat energy can be converted back to the same amount of potential energy. Without this, we can’t exactly say that energy is conserved. For all we know, some energy might have disappeared – meaning not conserved.
I believe some scientists must have done this. Following in Galileo’s footsteps, let me suggest a simple way using this setup.
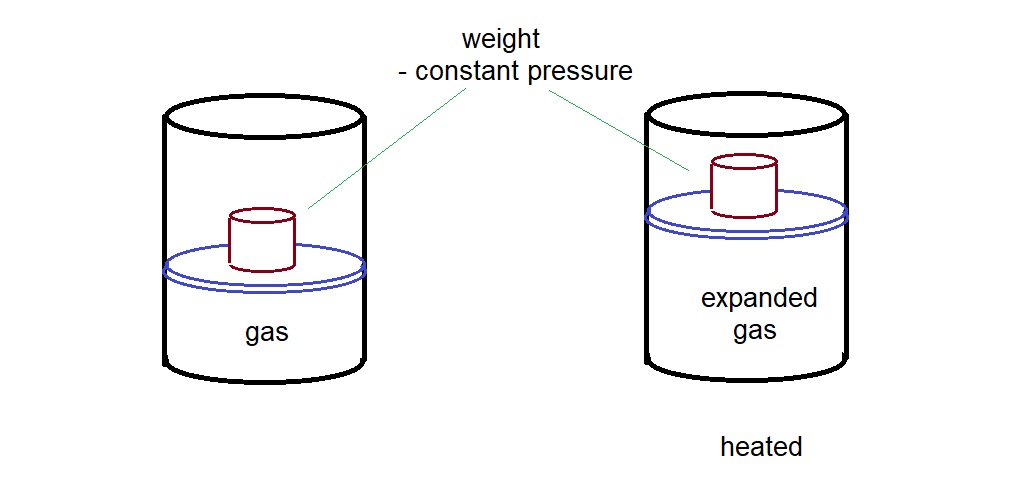
A weight sits the on sliding lid of a gas container. When heated, the gas expands and pushes up the weight. This increases the potential energy of the weight.
Today, this is quite easily setup. It might not have been easy to design such a measurement in the 19th century but should be possible with some effort.
The idea of conservation of energy tells us that
Heat into the gas = increase in potential energy of the weight + increase in internal energy of the gas
If you have followed this article so far, then you had a glimpse at the ingenious and painstaking effort scientists had gone through to discover all these things about physics.
Today, scientists and textbooks accept the law of conservation of energy :
Energy cannot not be created or destroyed, and can only be converted from one form to another.
(As long we are not talking about the atomic bomb and nuclear energy.)
You can learn these concepts and more at Dr Hock's maths and physics tuition.